Κωνικές τομές με τις σφαίρες του Dandelin

Δρ. Νίκος Σωτηρόπουλος, Μαθηματικός

Κωνική τομή ονομάζεται μία καμπύλη που προκύπτει από την τομή ενός κώνου και ενός επιπέδου, ή ακριβέστερα, από την τομή ενός επιπέδου με δύο ίσες ορθές άπειρες κωνικές επιφάνειες που έχουν κοινό άξονα και συνδέονται στην κορυφή τους (ο ένας κώνος εφαρμόζει "αναποδογυρισμένος" πάνω στην κορυφή του άλλου). Όλες οι καμπύλες το πολύ δεύτερης τάξης στο επίπεδο είναι κωνικές τομές. Η γενική εξίσωση μιας κωνικής τομής είναι:

Η επόμενη μικροεφαρμογή (Java applet) σας επιτρέπει να κατανοήσετε τις κωνικές τομές. Συγκεκριμένα, ποιες καμπύλες προκύπτουν από την τομή ενός επιπέδου με ένα κώνο (δίχωνο). Επιπλέον, σας δίνει την ευκαιρία να δείτε και να κατανοήσετε την απόδειξη του Dandelin, δηλαδή ότι η έλλειψη, η παραβολή και η υπερβολή είναι κωνικές τομές. Διαβάστε τις παρακάτω οδηγίες και  ασχοληθείτε λίγο με το applet. Προσπαθήστε να κάνετε αυτή την απόδειξη. Αν δεν το επιτύχετε, δείτε παρακάτω την απόδειξη που σας προτείνουμε.

Οδηγίες για την εργασία με το applet.

  Αν δε βλέπετε τίποτα, τότε πρέπει να εγκαταστήσετε την Java κάνοντας κλικ πάνω στο εικονίδιο.
 

Επιλέξτε ένα από τα κουμπιά στα δεξιά του πίνακα για να παραχθεί η κωνική τομή που θέλετε. Για να αλλάξετε την οπτική γωνία, κρατήστε πατημένο το αριστερό πλήκτρο του ποντικιού στην περιοχή σχεδίασης και σύρετε. Για να εμφανιστούν οι σφαίρες του Dandelin, επιλέξτε "Εμφάνισε την κατασκευή του Dandelin". Αν στη συνέχεια μετακινήστε το ποντίκι σας πάνω από οποιοδήποτε σημείο της κωνικής, θα εμφανιστεί ολόκληρη η κατασκευή του Dandelin για το σημείο αυτό. Κάντε κλικ στην εικόνα, αν θέλετε να αφαιρέσετε το επιλεγμένο σημείο. Οι υπόλοιποι δύο έλεγχοι μπορούν να χρησιμοποιηθούν για την αλλαγή της κλίσης και της θέσης του επιπέδου που τέμνει τον κώνο.

Ο Germinal Pierre Dandelin (12 Απριλίου 1794 - 15 Φεβρουαρίου 1847) ήταν ένας μαθηματικός Γαλλο-Βελγικής καταγωγής. Το 1822 απέδειξε με κομψό τρόπο ότι η έλλειψη, η υπερβολή και η παραβολή παράγονται από μια τομή ενός κώνου με ένα επίπεδο. Οι σφαίρες εγγράφονται σε έναν κώνο και εφάπτονται σε δύο σημεία στο επίπεδο που τέμνει τον κώνο. Τα σημεία αυτά αποτελούν τις εστίες της κωνικής τομής. Στη συνέχεια παρουσιάζονται οι τρεις αποδείξεις του Dandelin.
Τι σημαίνει να αποδειχτεί ότι η καμπύλη είναι έλλειψη, υπερβολή ή παραβολή;
Πριν αποδειχτεί ότι οι κωνικές τομές, που παράγονται στην παραπάνω μικροεφαρμογή (applet), είναι ελλείψεις, υπερβολές ή παραβολές, αξίζει να αφιερώσετε λίγο χρόνο για να κατανοήσετε τι πρόκειται να αποδειχτεί. Το μόνο που χρειάζεται να κάνετε είναι να δείξετε ότι μια υπό εξέταση κωνική τομή ικανοποιεί τον ορισμό της έλλειψης, της υπερβολής ή της παραβολής.  Για μια γρήγορη υπενθύμιση των ορισμών της έλλειψης, υπερβολής και παραβολής, κάντε κλικ στον προηγούμενο σύνδεσμο.

Η απόδειξη του Dandelin για την έλλειψη (Δείτε επίσης μια πιο εύκολη απόδειξη για την έλλειψη σε κύλινδρο.)

Επιλέξτε το κουμπί επιλογής Έλλειψη στη μικροεφαρμογή.

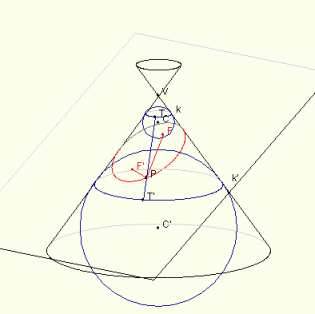
Στη συνέχεια, επιλέξτε Εμφάνισε την κατασκευή του Dandelin. Θα πρέπει να δείτε δύο σφαίρες στην εικόνα. Το κέντρο της πρώτης σφαίρας είναι στο σημείο C, ενώ το κέντρο της δεύτερης σφαίρας είναι στο σημείο C'. Τα σημεία επαφής της άνω σφαίρας με την εσωτερική επιφάνεια του κώνου σχηματίζουν τον κύκλο (κ) και η σφαίρα εφάπτεται στο επίπεδο από πάνω σε ένα σημείο F. Ομοίως, η κάτω σφαίρα εφάπτεται στην εσωτερική επιφάνεια του κώνου και τα σημεία επαφής σχηματίζουν τον κύκλο (k').Επιπλέον, η σφαίρα αυτή εφάπτεται στο επίπεδο από κάτω σε ένα σημείο F'. Τα δύο σημεία F και F' είναι οι δύο εστίες της σχηματιζόμενης έλλειψης. Τοποθετήστε το δείκτη του ποντικιού σας πάνω από οποιοδήποτε σημείο της κωνικής τομής (εμφανίζεται με κόκκινο χρώμα). Με αυτόν τον τρόπο μπορείτε να επιλέξετε ένα σημείο, το οποίο θα φέρει την ένδειξη P. Το applet θα εμφανίσει κάποια επιπλέον σημεία και γραμμές. Τα δύο νέα σημεία Τ και Τ' είναι τα σημεία τομής της γραμμής PV με τους κύκλους k και k', αντίστοιχα.

Στη συνέχεια θα αποδειχτεί ότι η καμπύλη που προέκυψε ως τομή μιας κωνικής επιφάνειας και ένα επίπεδο στην παραπάνω εικόνα είναι μία έλλειψη. Θεωρείστε ένα αυθαίρετο σημείο P της καμπύλης. Θα δειχτεί ότι το άθροισμα των αποστάσεών του από τα σημεία F και F' είναι σταθερό, ανεξάρτητα από τη θέση του σημείου Ρ της καμπύλης. Αυτό, σύμφωνα με τον ορισμό, θα σημαίνει ότι η καμπύλη είναι μία έλλειψη.

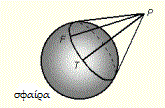
(1) Παρατηρείστε ότι (PF) = (PT). Γιατί; Και τα δύο σημεία F και Τ βρίσκονται σε δύο διαφορετικές ευθείες από το σημείο Ρ. Το πρώτο αγγίζει την επάνω σφαίρα στο F και το δεύτερο αγγίζει την ίδια σφαίρα στο Τ. Φανταστείτε όλες αυτές τις ευθείες που ξεκινούν από Ρ και εφάπτονται στην επάνω σφαίρα. Όλες αυτές οι ευθείες θα σχηματίσουν ένα "κωνικό καπέλο" της άνω σφαίρας. Είναι λοιπόν εύκολο να δει κανείς ότι οι αποστάσεις του σημείου P από όλα τα σημεία επαφής στην επάνω σφαίρα είναι ίσες. Αυτό σημαίνει ότι και οι αποστάσεις (PF) και (PT)είναι ίσες (βλέπε σχήμα).

(3) Εφόσον (PF) = (PT) και (PF') = (PT'), είναι πλέον προφανές ότι (PF) + (PF') = (PT) + (PT'). Αλλά τα σημεία T, P, και T' είναι σημεία της ευθείας  VP η οποία διέρχεται από την κορυφή V του κώνου οπότε (PT) + (PT') = (TT').

Επιλέγοντας ένα άλλο σημείο P επάνω στην υπό διερεύνηση καμπύλη καταλήγετε σε δύο διαφορετικά σημεία T και  T'. Παρατηρείστε ότι  το τμήμα (TT') παραμένει σταθερό, διότι ισούται με την απόσταση των δύο κύκλων k και k' η οποία μετρείται στην επιφάνεια του κώνου. Αυτή η απόσταση είναι σταθερή. Έτσι διαπιστώνετε ότι η καμπύλη αυτή είναι έλλειψη.
 

Η απόδειξη του Dandelin για την υπερβολή

Επιλέξτε το κουμπί επιλογής Υπερβολή στη μικροεφαρμογή.

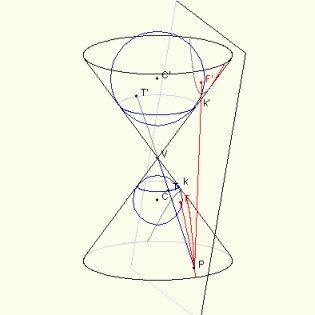
Στη συνέχεια, επιλέξτε Εμφάνισε την κατασκευή του Dandelin. Θα πρέπει να δείτε δύο σφαίρες στην εικόνα. Το κέντρο της πρώτης ένα είναι στο σημείο C που βρίσκεται κάτω από την κορυφή του κώνου V, ενώ το κέντρο της δεύτερης ένα είναι στο σημείο C' βρίσκεται πάνω από το V. Η κάτω σφαίρα εφάπτεται στην εσωτερική επιφάνεια του κώνου και τα σημεία επαφής σχηματίζουν τον κύκλο k, επίσης η σφαίρα αυτή εφάπτεται στο επίπεδο που τέμνει τον κώνο στο σημείο F. Ομοίως, η επάνω σφαίρα εφάπτεται στην κωνική επιφάνεια σχηματίζοντας τον κύκλο k', επίσης εφάπτεται και στο επίπεδο που τέμνει τον κώνο στο σημείο F'. Τα δύο αυτά σημεία F και F 'είναι οι δύο εστίες της σχηματιζόμενης υπερβολής. Τώρα, τοποθετήστε το δείκτη του ποντικιού σας πάνω από οποιοδήποτε σημείο της κωνικής τομής. Με αυτόν τον τρόπο μπορείτε να επιλέξετε ένα σημείο, το οποίο θα φέρει την ένδειξη P. Το applet θα εμφανίσει τώρα και κάποια επιπλέον σημεία και  γραμμές. Τα δύο νέα σημεία Τ και Τ' είναι τα σημεία τομής της ευθείας PV με κύκλους k και k', αντίστοιχα. Τα σημεία αυτά είναι τα σημεία τομής της ευθείας PV με τους δύο κύκλους k και k'.

Στη συνέχεια θα αποδειχτεί  ότι η καμπύλη που προέκυψε από την τομή της κωνικής επιφάνειας με ένα επίπεδο, στην παραπάνω εικόνα, είναι μία υπερβολή. Θεωρείστε ένα αυθαίρετο σημείο P του κάτω κλάδου καμπύλης. Θα δείξουμε ότι η διαφορά των αποστάσεών του από τα σημεία F και F' είναι σταθερό, ανεξάρτητα από την θέση του σημείου Ρ της καμπύλης. Αυτό, σύμφωνα με τον ορισμό, θα σημαίνει ότι η καμπύλη θα είναι μία υπερβολή.

Όμοια, όπως και στην περίπτωση της έλλειψης, μπορείτε να παρατηρήσετε ότι (PF) = (PT) και (PF') = (PT').  Ως εκ τούτου (PF') – (PF) = (PT') – (PT). Αλλά τα σημεία T, P, και T' είναι σημεία της ίδιας ευθείας VP, η οποία διέρχεται από την κορυφή V του κώνου. Εφόσον τα σημεία αυτά βρίσκονται εκατέρωθεν του σημείου V, εύκολα διαπιστώνετε ότι  (PT') – (PT) = (T'T).

Επιλέγοντας μια διαφορετική θέση του P στον κάτω κλάδο της καμπύλης οδηγήστε σε δύο διαφορετικά σημεία  T και T'. Η απόσταση  (TT') όμως παραμένει η ίδια, διότι είναι η απόσταση μεταξύ των κύκλων   k και k', η οποία μετρείται στην επιφάνεια του κώνου. Αυτή η απόσταση είναι σταθερή. Με τις ίδιες ακριβώς σκέψεις και παρατηρήσεις εάν επιλέξετε ένα σημείο P στον επάνω κλάδο της υπό διερεύνηση καμπύλης διαπιστώνετε ότι η διαφορά (PF) – (PF') είναι σταθερή. Έτσι διαπιστώνετε ότι η καμπύλη είναι υπερβολή.
 

Η απόδειξη του Dandelin για την παραβολή

Επιλέξτε το κουμπί επιλογής Παραβολή στη μικροεφαρμογή.

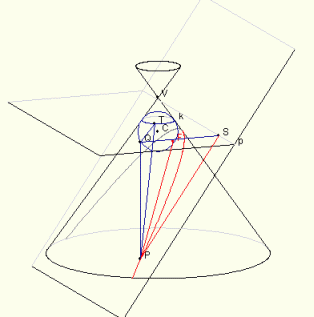
Στη συνέχεια, επιλέξτε Εμφάνισε την κατασκευή του Dandelin. Θα πρέπει να δείτε μία σφαίρα στην εικόνα. Το κέντρο αυτής της σφαίρας είναι στο σημείο C και βρίσκεται κάτω από τον κορυφή του κώνου V. Η σφαίρα εφάπτεται στην εσωτερική επιφάνεια του κώνου και στο επίπεδο που τέμνει τον κώνο στο σημείο F.  Επιπλέον, στην εικόνα εμφανίζεται και ένα δεύτερο επίπεδο, το οποίο είναι σταθερό εφόσον παραμένει συνεχώς κάθετο στον άξονα του κώνου και τέμνει τη σφαίρα κατά τον κύκλο k. Παρατηρήστε ότι ο κύκλος k αποτελείται από τα σημεία επαφής της σφαίρας και του κώνου. Η τομή των δύο αυτών επιπέδων είναι η ευθεία (p) , η οποία είναι σταθερή εφόσον είναι τομή δύο σταθερών επιπέδων. Θα αποδειχτεί ότι η ευθεία αυτή είναι η διευθετούσα της σχηματιζόμενης παραβολής και το σημείο F ότι είναι η εστία της παραβολής. Τοποθετήστε τον κέρσορα του ποντικιού επάνω σε ένα οποιοδήποτε σημείο της κωνικής τομής. Εμφανίζεται ένα σημείο με το γράμμα Ρ. Η μικροεφαρμογή εμφανίζει τρία επιπλέον σημεία και κάποια ευθύγραμμα τμήματα. Το σημείο Τ είναι το σημείο τομής της ευθείας PV με τον κύκλο k. Το σημείο Q είναι η κάθετη προβολή του σημείου Ρ στο επίπεδο του κύκλου k. Το τρίτο σημείο S είναι το ίχνος της καθέτου από το σημείο Ρ στην ευθεία p.

Στη συνέχεια θα αποδειχτεί ότι η καμπύλη που προκύπτει από την τομή της κωνικής επιφάνειας και ενός επιπέδου το οποίο είναι παράλληλο σε μία γενέτειρα του κώνου είναι μια παραβολή. Θεωρείστε ένα τυχαίο σημείο P της καμπύλης. Θα αποδειχτεί ότι η απόσταση του P από το σταθερό σημείο F ισούται με την απόστασή του από την ευθεία p ανεξάρτητα από τη θέση του σημείου P. Συνεπώς, σύμφωνα με τον ορισμό, αυτό σημαίνει ότι η καμπύλη είναι παραβολή.

Όμοια, όπως και στην περίπτωση της έλλειψης, είναι (PF) = (PT). Αυτό σημαίνει ότι αρκεί να δειχτεί ότι (PT) = (PS). Τα ευθύγραμμα τμήματα PT και PS είναι οι υποτείνουσες των ορθογωνίων τριγώνων PQT και PQS. Αυτά τα τρίγωνα είναι ίσα, διότι έχουν την κάθετη πλευρά PQ κοινή  και τις  οξείες γωνίες PSQ και  PTQ ίσες. Γιατί οι οξείες γωνίες  PSQ  και  PTQ είναι ίσες; Να γιατί: όταν η τομή ενός επιπέδου και ενός κώνου είναι παραβολή τότε το επίπεδο έχει μια πολύ συγκεκριμένη θέση σε σχέση με τον κώνο. Η γωνία-κλίση που σχηματίζει το επίπεδο που τέμνει τον κώνο με οποιοδήποτε οριζόντιο επίπεδο (κάθετο στον άξονα του κώνου) είναι ίση με τη γωνία που σχηματίζεται από οποιαδήποτε ευθεία η οποία βρίσκεται στην επιφάνεια του κώνου και διέρχεται από την κορυφή του P (γενέτειρα) με το οριζόντιο επίπεδο. Οι γωνίες PTQ και PSQ είναι τέτοιες γωνίες, άρα είναι ίσες.

Συνοψίζοντας τα ανωτέρω, έχουμε: (PF) = (PT) = (PS) = d(P, p). Αυτό σημαίνει ότι η απόσταση τυχαίου σημείου P της υπό μελέτη καμπύλης από το σημείο F είναι ίση με την απόστασή του από την ευθεία p. Επομένως, η καμπύλη είναι παραβολή με εστία το σημείο F και διευθετούσα την ευθεία p.
 

mathforum.org